材料的力学性能
仅供学习交流使用,内容来自2025年秋季学期。本人不对本文中的图片保有版权。
公式没渲染出来的话刷新一下网页就好了。
受力形变
形变,就是材料的形状和体积对于外力的响应。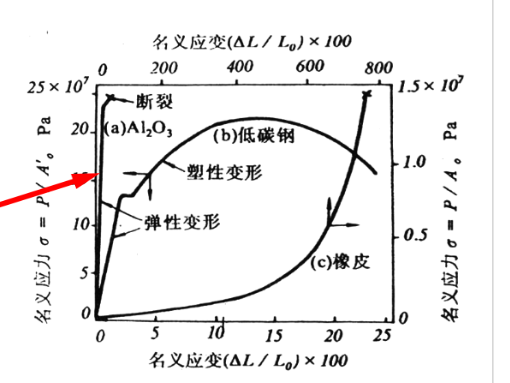
- 脆性材料:只有弹性变形阶段,几乎不发生塑性变形,超过弹性极限后断裂。绝大多数无机材料是这种变形行为,总弹性形变能很小
- 延性材料:开始为弹性变形,接着有一段塑性变形,总变形能很大。如低碳钢。
- 弹性材料:具有极大的弹性形变,没有残余形变。如橡胶
当作用力较小时,$\sigma<\sigma_s$,发生可逆的弹性形变;作用力超过$\sigma_s$,则发生不可逆的塑性形变。高温恒应力下发生蠕变。
基本力学行为
受力$\to$ 弹性形变$\to$ 塑性形变$\to$ 断裂
基本力学指标包括强度,塑性,韧性。
- 屈服强度 $\sigma_s$
- 抗拉强度 $\sigma_b$
- 延伸率$\delta$
- 断面收缩率$\psi$

应力
$$\sigma=\frac{F}{A}$$
名义应力:A选用受力前的初始面积。实际一般用名义应力。
真实应力:A选用受力后的真实面积。
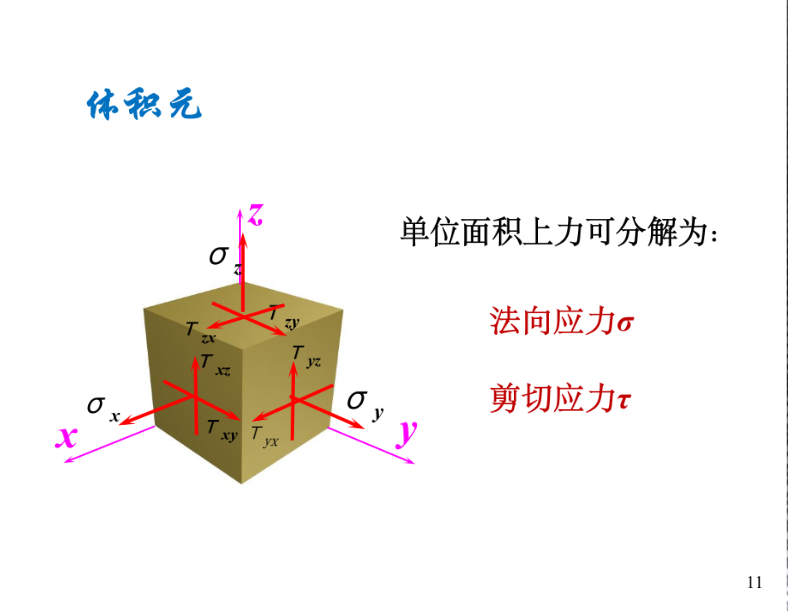
规定:
- 应力分量下标第一个字母表示作用面的法向方向,第二个字母表示应力作用的方向。法向应力可以略去一个。
- 拉应力(产生正应变)为正,压应力为负
应变
物体内部各质点相对位移量
$$\varepsilon=\frac{\Delta L}{L}$$
法向应变
$\varepsilon$称为名义应变。真实应变为$\varepsilon_{true}=\ln\frac{L_1}{L_0}$
一般都使用名义应变。
剪应变
剪应力作用下产生的应变,是体积元上两个面夹角的变化。
压缩应变
受到流体的静压力作用而产生压缩应力,压缩应变$\Delta=\frac{\Delta V}{V_0}$
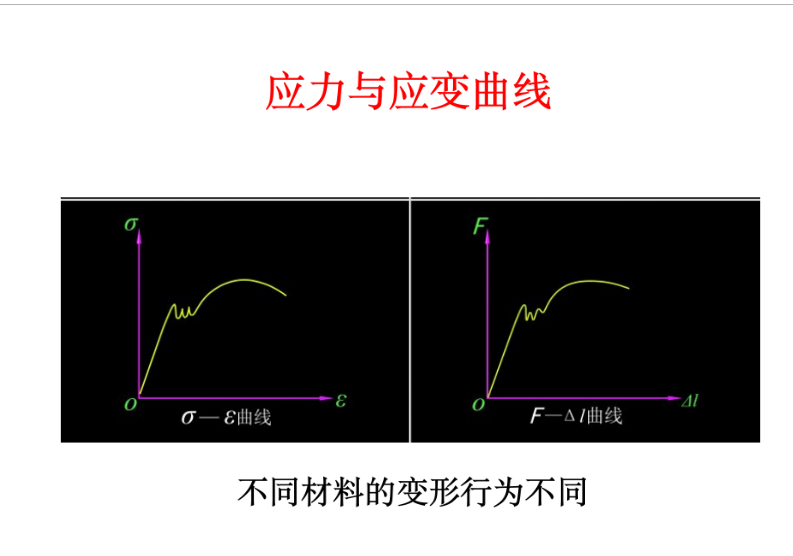
低碳钢的典型$\sigma-\varepsilon$曲线
弹性形变
外力去除后形变完全消失的称为弹性形变。
- 可逆性
- 线性(单值,胡克定律)
- 变形量较小
高分子材料的弹性形变一般都为非线性的。而常见金属的弹性形变和结晶态高分子的弹性变形量很小(1%)。
单向应力状态
各向同性的长方体沿x轴受到拉力
$$\varepsilon=\frac{\Delta L}{L}=\frac{\sigma_x}{E}$$
E为弹性模量
横向发生收缩,引入横向变形系数$\mu$,称为泊松比。
$$\mu=\vert\frac{\varepsilon_y}{\varepsilon_z}\vert=\vert\frac{\sigma_z}{\sigma_x}\vert$$
金属材料的泊松比约为0.3,陶瓷约为0.2。
三向应力状态
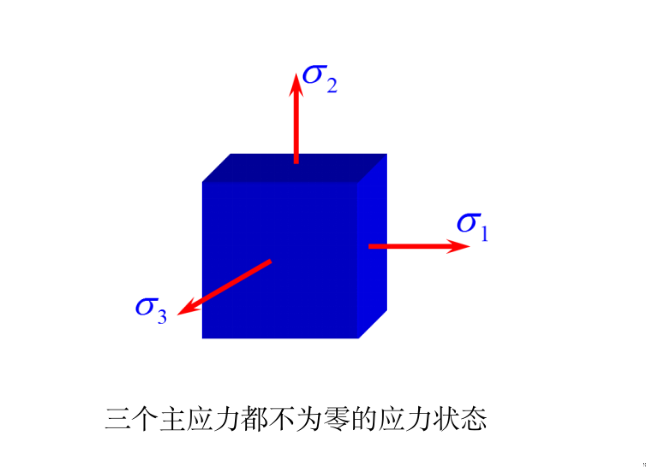
各方向总应力是分量的线性叠加。
$$\varepsilon_1=\frac{\sigma_1}{E}+-\mu\frac{\sigma_2}{E}+-\mu\frac{\sigma_3}{E}$$
此时胡克定律即为
$$\varepsilon_x=\frac{1}{E}[\sigma_x-\mu(\sigma_y+\sigma_z)]$$
另外两个方向同理
剪切应变
$$\gamma_{xy}=\frac{\tau_{xy}}{G}$$
G为剪切模量
$$G=\frac{E}{2(1+\mu)}$$
对于各向异性的材料,不满足胡克定律。而要用广义胡克定律描述。
弹性变形的本质
在外力作用下,构成材料的原子从平衡位置产生可逆位移
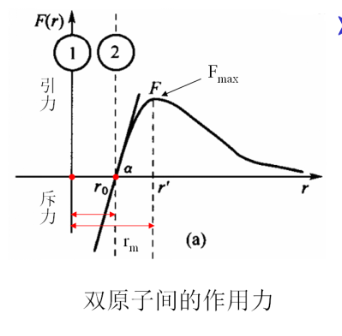
弹性模量的本质
弹性模量E越大,材料刚性越强,越不易产生变形。
从原子尺度看,弹性模量是原子键合强度的标志,与原子间结合力曲线的一阶导数有关。

弹性模量表征材料对弹性变形的抵抗力。工程上称为刚度。但是弹性模量是材料的本征参数,而实际工件的抗变形能力还与尺寸和载荷等有关,因此二者不能简单等同。
弹性模量的影响因素
- 键合方式:键合方式越强,弹性模量越大。
- 温度升高,原子间距增大,作用力减小,弹性模量降低
- 应力:压应力使得原子间距减小,弹性模量增大。张应力使得原子间距增大,弹性模量减小。
- 化学组成
- 合金的弹性模量随组成元素的质量分数、组织结构、晶体结构的变化而变化
- 固溶体合金的E主要取决于溶剂元素的性质和晶体结构。
- 微观组织
- 金属的弹性模量对组织不敏感,钢的热处理能显著提高强度,但是E变化不是很大
- 陶瓷的弹性模量随气孔率增高下降,经验公式有
$$E=E_0(1-1.9p+0.9p^2)$$,p 为气孔率
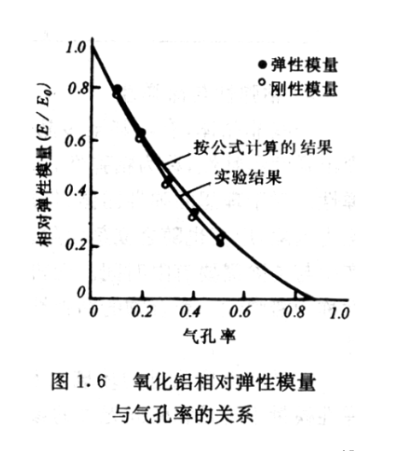
- 高分子材料的弹性模量可通过添加剂提高
实际多组元体系的弹性模量介于高弹性模量和低弹性模量之间。
假定体系内应力均匀
- 两相系统泊松比和应变相同,得到上限弹性模量
$$E_U=E_1V_1+E_2V_2$$
$V_i$为对应的体积分数
2.假定泊松比和应力相同,得到下限弹性模量
$$\frac{1}{E_L}=\frac{V_1}{E_1}+\frac{V_2}{E_2}$$
- 原子结构
-金属元素的原子半径越大,E越小- 过渡元素的弹性模量较大,因为其原子半径较小,且d层电子引起较大的原子间结合力
- 晶体结构
- 单晶的E各向异性
- 多晶的E伪各向同性
- 玻璃态的E各向同性
粘弹性和滞弹性
实际材料的与时间有关的弹性成为滞弹性。应变滞后于应力。
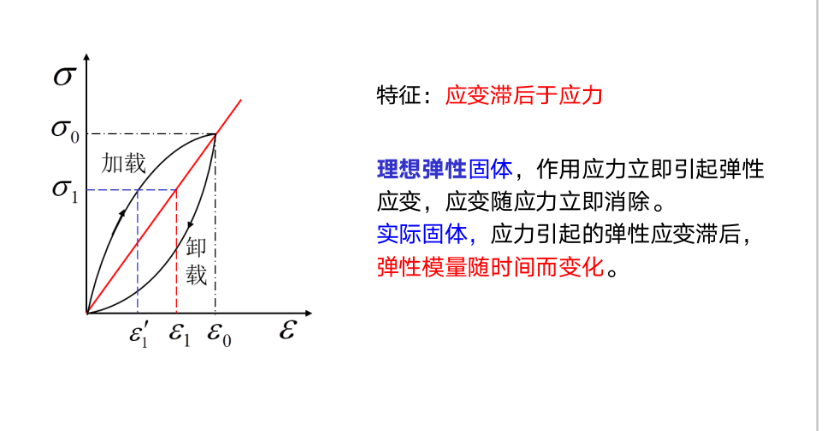
可以用弹性元件和粘性元件的组合模拟这种力学行为。
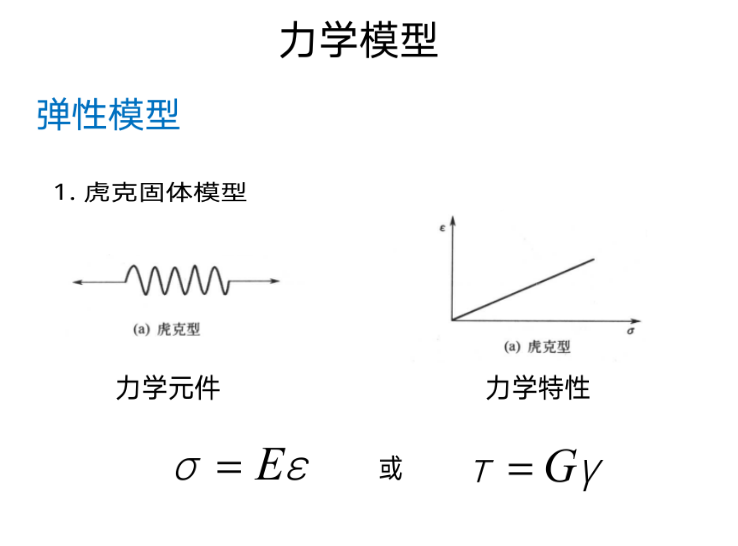
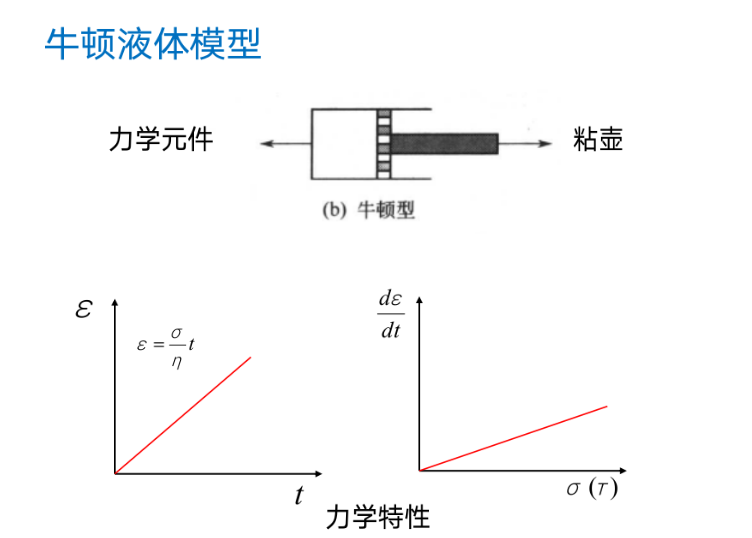
弹性元件$\sigma=E\varepsilon$,粘性元件$\sigma=\eta \frac{\mathrm{d}\varepsilon}{\mathrm{d}t}$
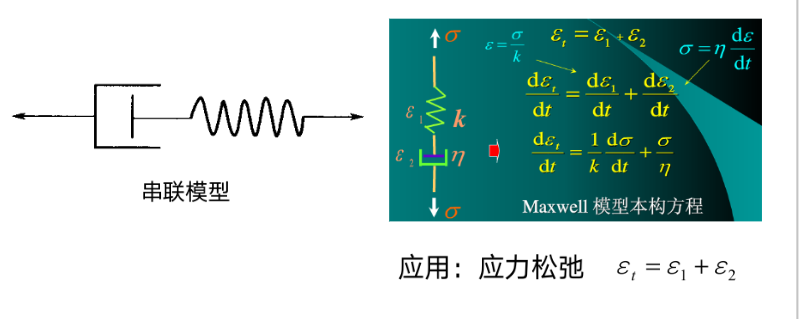
麦克斯韦模型
麦克斯韦液体是液态粘弹性液体,由弹簧和粘壶串联
应用:应力松弛。$\varepsilon=\varepsilon_1+\varepsilon_2$
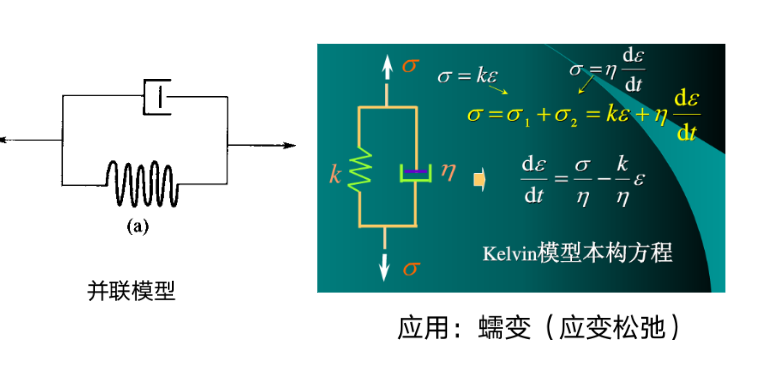
开尔文固体模型
描述固体粘弹性行为,并联,$\sigma=\sigma_1+\sigma_2$
应用:蠕变(应变松弛)
一些材料(如高温下的玻璃或高分子)在小应力下同时表现出粘性和弹性,称为粘弹性。可以认为是充分发展的滞弹性。
松弛
应变松弛(蠕变)
材料在恒应力下变形缓慢增加,如沥青等的膨胀。(并联模型)
$$E_c(t)=\frac{\sigma_0}{\varepsilon(t)}$$
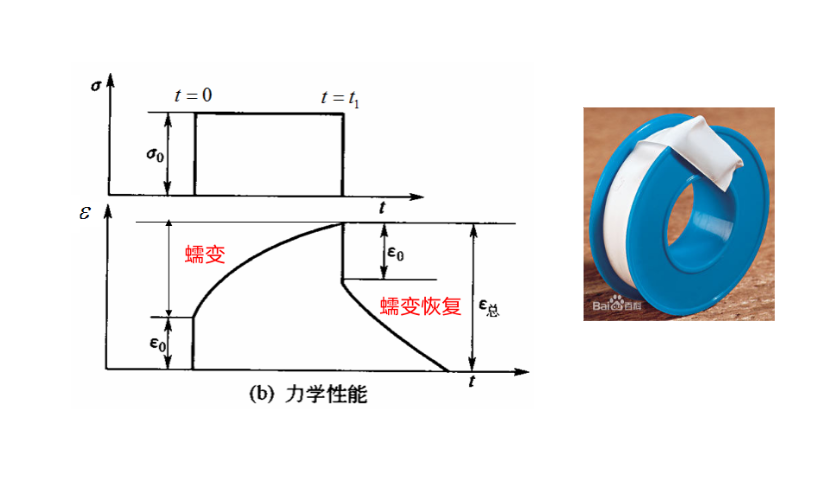
应力松弛(弛豫)
在持续外力下发生变形,总变形量不变,由于粘性的徐变变形增加,使得弹性变形减小,应力下降。(串联模型)
$$E_{\tau}=\frac{\sigma(t)}{\varepsilon_0}$$
一般来说,弛豫的来源是玻璃相
塑性形变
材料经过塑性形变而不失效的能力称为延展性,是重要的力学性能。
指标:
- 断裂伸长率(延伸率):$\delta=\frac{\Delta l}{l_0}\times 100%$
- 断面收缩率 :$\psi=\frac{\Delta A}{A_0}$
只有极少数离子晶体在常温下有延展性,如AgCl可以冷轧,KCl晶体可以弯曲。他们都属于NaCl型结构。
四方$ZrO_2$晶体掺有少量$CeO_2$后在一定压力下发生相变(转为单斜晶系)而出现很大的塑性变形能力,称为超塑性或相变塑性。
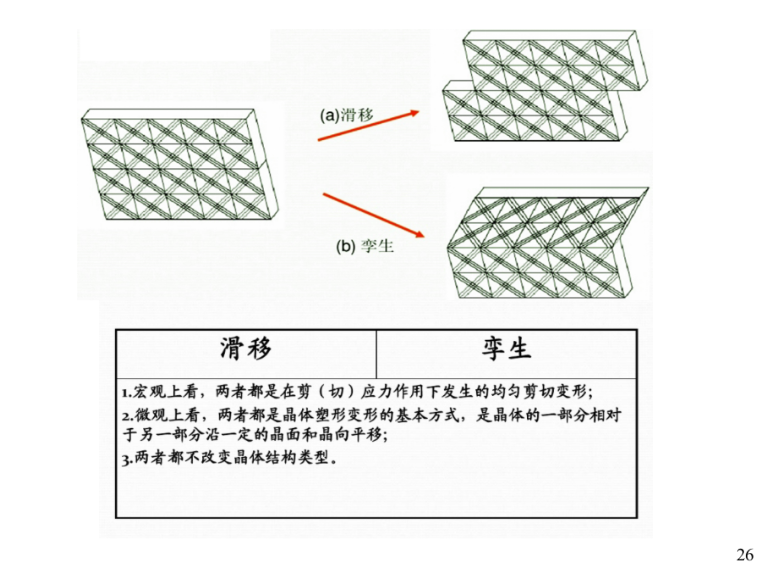
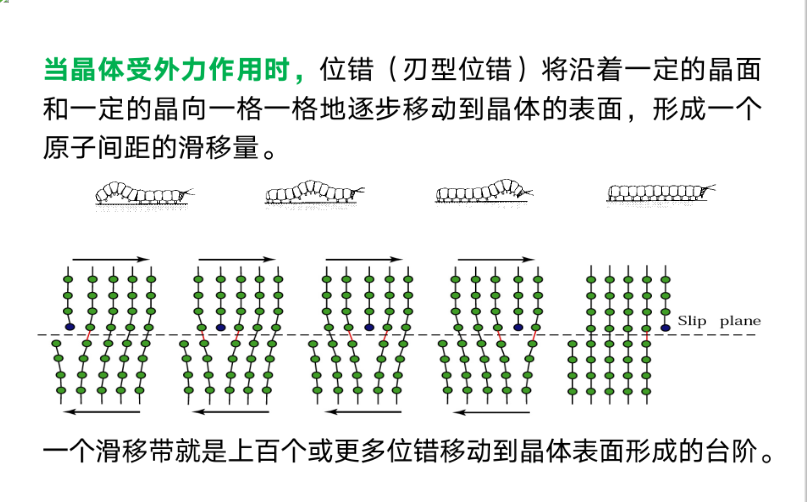
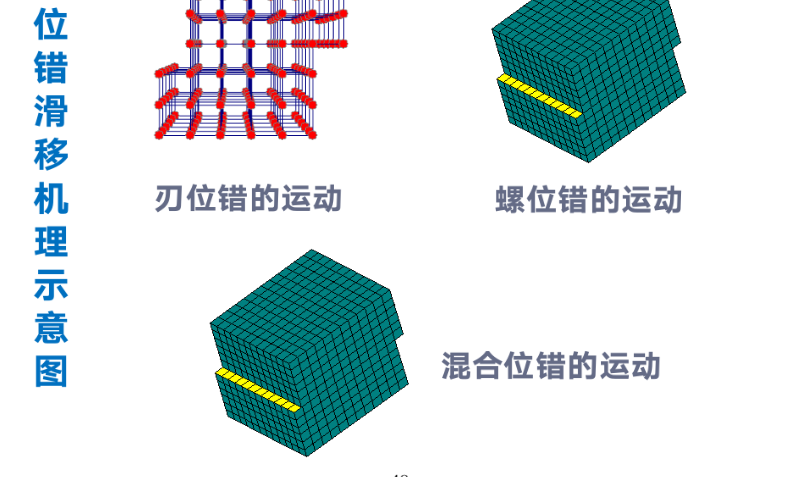
滑移在晶体中更常见,对变形的贡献更大。
滑移只发生在特定的晶面和晶向上。
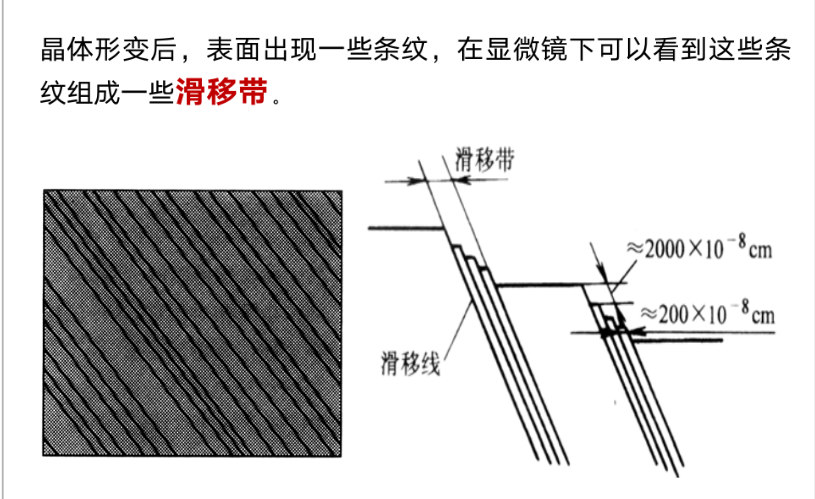
滑移面和滑移方向一般为密排面和密排方向。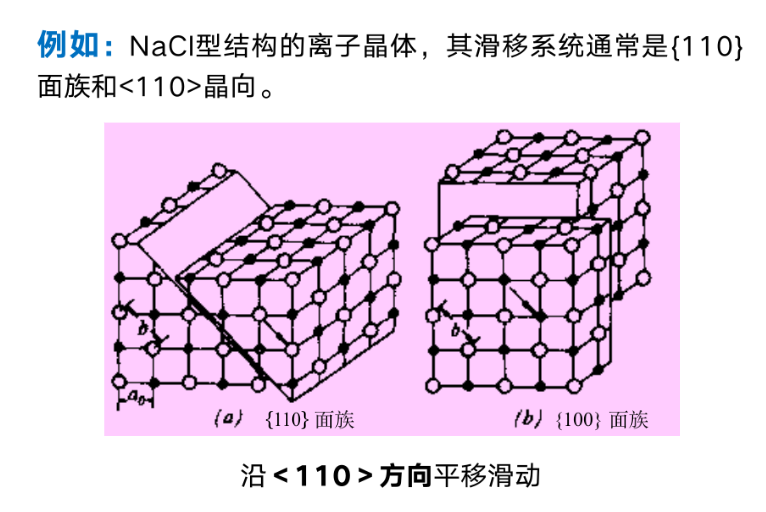
滑移系数目越多,塑性越好
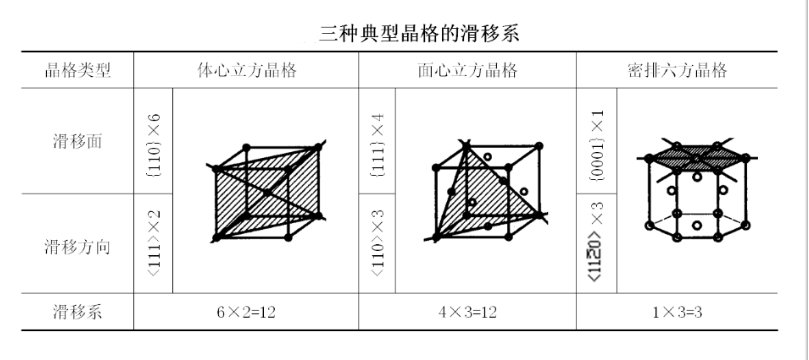
滑移方向的权重更高,所以fcc的塑性更好。
多晶材料不易滑移,晶界对于滑移有钉扎作用。
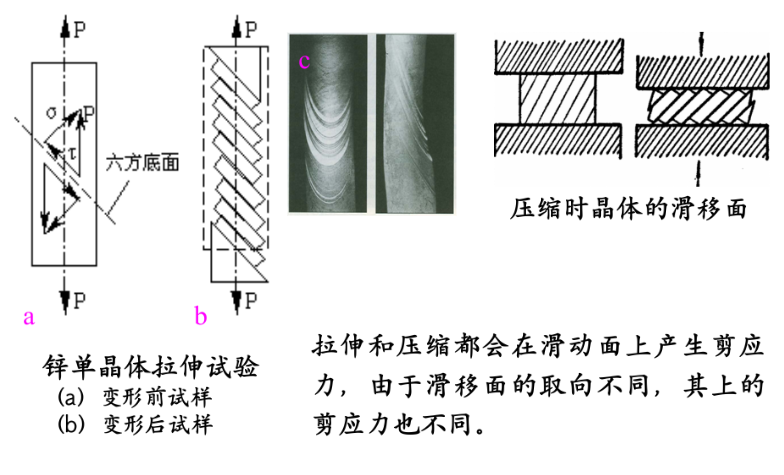
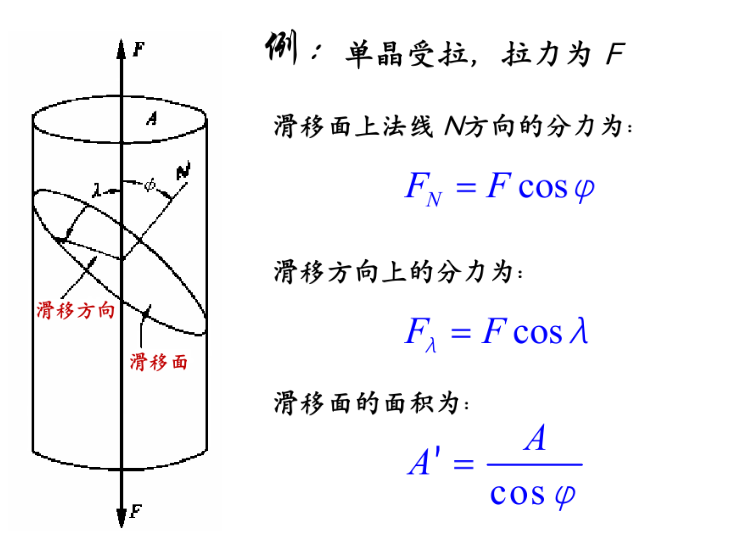
法线上应力$\sigma=\frac{F}{A}\cos^2\varphi$,滑移方向上剪应力为$\tau=\frac{F}{A}\cos\lambda\cos\varphi$
剪应力大于临界值发生滑移
塑性形变指数

高温蠕变
材料在高温和低于屈服强度的应力下随时间产生塑性变形。
高温
- 金属 $T>0.3\sim 0.4 T_m$,$T_m$为熔点
- 陶瓷 $T>0.4\sim 0.5 T_m$
- 高分子 $T>T_g$,大于玻璃化转变温度
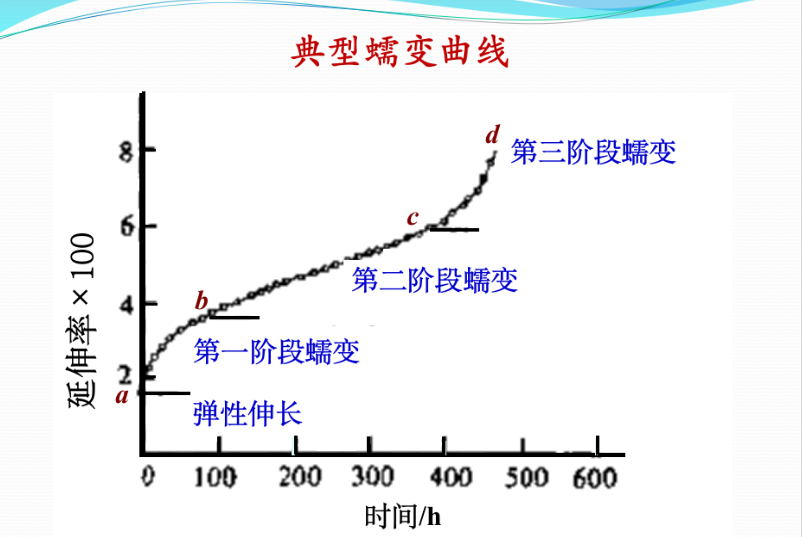
- 起始阶段:普通线弹性
- 减速阶段